Assignment 6
AX = XY=YB

by
Jenny Johnson

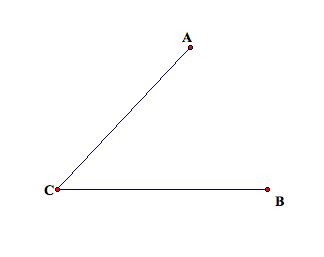
In this exploration, we are given three non-collinear points A, B and C. We connect A to C and B to C to form the following figure.

The point of the exploration is to find a point X on AC and a point Y on BC such that AX = XY = YB. So we want to find the points X and Y so the three segments mentioned are congruent. An example of points X and Y are shown in the following diagram.

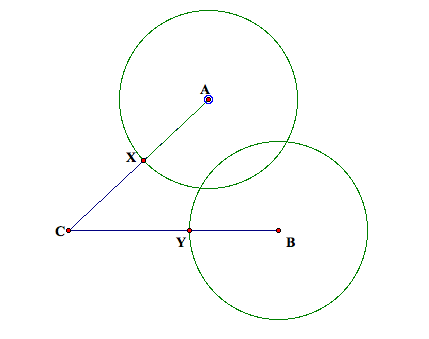
My first exploration to find the points X and Y was to draw circles. Any two circles with the same radius and centers at A and B will give us respective lengths of potential AX and BY such that AX = YB. So, I drew a circle centered at A with an arbitrary radius. The intersection of the circle with the segment AC I labeled X. Then, I constructed a circle centered at B with radius AX. The intersection of this circle with segment BC I labeled Y. Thus, by construction AX = YB.

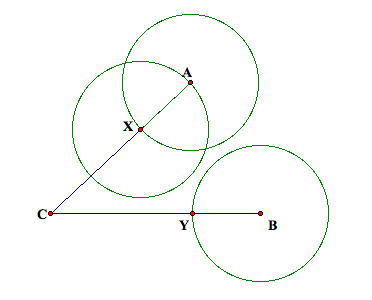
Now I can drag X along the line segment AC and the point Y also adjusts so that AX = YB. I then constructed a circle centered at X with radius XA.

I can drag X until the circle centered at X with radius XA intersects the point Y. Then the radius of the circle is XY, which means XY = XA = YB at this point. A picture of this is shown below.

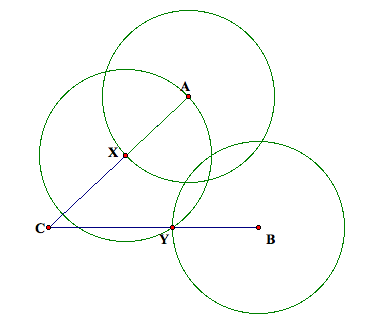
Thus, we have found a point X and a point Y such that AX = XY = YB.

To explore this GSP file, click here.

Return